Force sensing, molecular mechanics and cellular decisions
How do forces influence molecular interactions, and how does this determine cellular decisions. Each molecular interaction has a purpose in the cell. Every molecular interaction in the cell experiences a force due to thermal collisions of the molecule with other molecules, be it the solvent, metabolites or other proteins. This force provides the energy that drives two molecular entities close enough together to form a bond and apart again after a certain time elapsed that is proportional to the free energy difference of the bound and unbound state. Now there are some bonds which experience forces, deterministic ones, on top of these stochastic, thermal forces, e.g. during cell adhesion or activation of mechanosensitive ion channels (we will see below that an ion channel gate can be conceptualized as a single bond connected to its surrounding). These forces alter the time that the molecular bond remains bound, but not only is the magnitude but also the sign of the change different depending on the biological system that you look at. George Bell made the empiric observation that the time that bond remains stable under force, depends exponentially on the applied force.
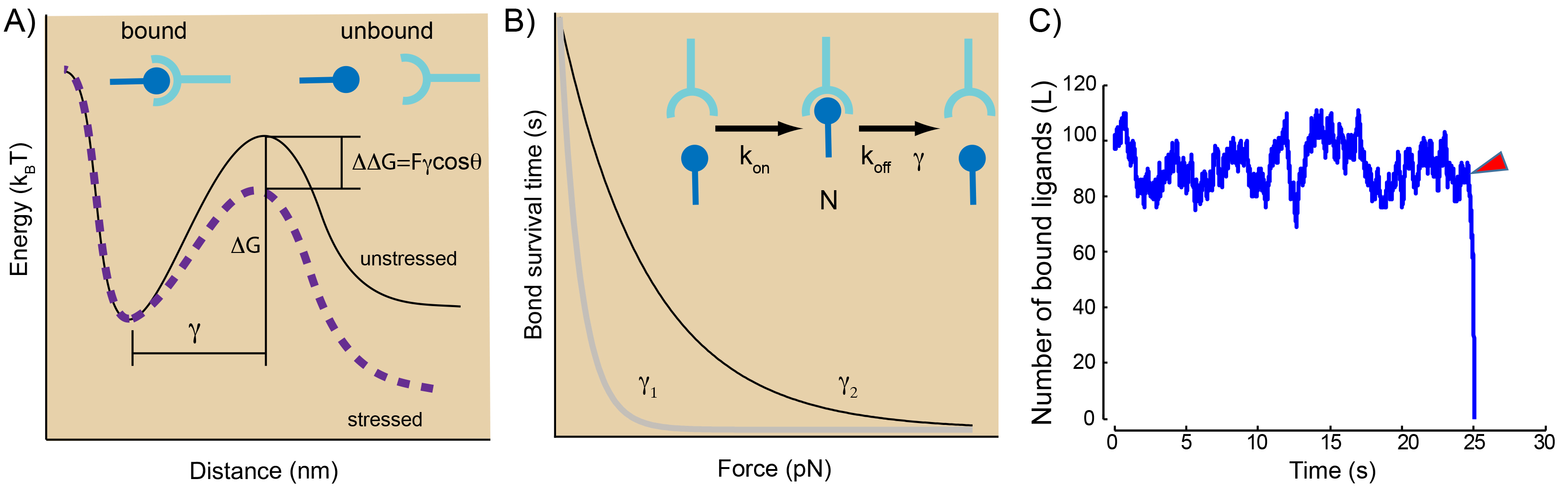
A: Conceptual display of an energy landscape for a slip bond under force. The bound state and unbound state are separated by an energy barrier of height ∆G. Application of a force tilts the landscape and reduces the barrier by ∆∆G = F · γ cos(θ), with γ as the distance of the transition state from the bound state and cos(θ) as the thermally averaged projection of the barrier along the direction of force.
B: Mean lifetime of an intermolecular bond subjected a constant force showing slip bod behavior. A single bound state in equilibrium with its unbound state. See text for explanation on parameters C: Simulation of the evolution of the number of bound ligands for a slip bond cluster under a sudden perturbation after 25 s (red arrowhead). The cluster fails immediately.
Slip bonds have the peculiar property that they react very quickly to force and can this govern very fast cellular decision. An example of these rapid decision can be found in mechanosensitive ion channels. In this example, slip bond interactions stabilize the closed gate and force is transferred to the ion channel via a slip bond interaction to the cytoskeleton.
A: State diagram of a hypothetical ion channel gate with interactions to the surrounding subjected to a force F. i) Without force, the transition the channel fluctuates stochastically between the closed and open state. Upon force, the transition is accelerated and the probability to adopt an open conformation increases exponentially. ii) At the same time, force accelerates the dissociation of the tether from the channel, but stabilizes the open conformation until the bonds survival time passed. This force dependent unbinding transition k2(F) happens slower than the channel opening k1. iii) After unbinding of the tether, the open conformation will immediately relax back into its closed state. iv Fast rebinding of the tether to the channel ensures that it is ready for a new signaling event. B: Hypothetical energy landscape of a force-sensitive ion channel interacting with its surrounding. The most stable state (ground state in absence of force) is the closed channel with a tether bound. The most stable configuration under force is the open configuration. As force is applied, the state of the system (channel-tether) travels through an energy landscape characterized by multiple valleys and ridges. The most unstable state is the open channel without a tether attached. C: Simulation of open probability and closed state probability according to the state diagram in (A). Solid lines represent the open state after a stimulation at t=0 calculated according to the law of mass action outlined in the kinetic scheme in A. D: Markov chain Monte Carlo simulation of 1000 ion channels subjected to a mechanical stimulation ≈50 ms. White depicts open state, beige the closed state. The average
open probability is shown below for three different tether unbinding rates.
We can simulate this behavior as two slip bonds in series with different force dependent offrates such that these two bonds react on different timescales to the force. What we observed is a behavior reminiscent of ion channel gating: A rapid increase in the open state probability, followed by a slower closing under the constant force as seen in adapting ion channels.
However, if all bonds were to behave like Bell bonds, or slip bonds as they are called informally, then how could we move and exert forces onto anything? How can two cells remain bound when they move around or assemble into an epithelium that gets stretched like our skin? Imagine, you pull on something and it comes off much faster than if you did not pull on it, like you push on a closed latch that suddenly opens. As I said, there are bonds in our body that are unavoidably subjected to force, such as the bonds that mediate adhesion between our cells. They experience force, even though no-one pulls on them directly, but rather, because other molecules in their surrounding keep electrostatically (negatively charged glyocalyx) and sterically (bulky surface coats) pushing the contacting cell apart. Puff, unbound. That this does not happen, can be attributed, at least partially to a counterintuitive phenomenon. We call 
it catch bond, and this phenomenon is similar to a chinese fingertrap: You put your finger inside the trap, pull on it, and the stronger you pull, the stronger the trap will trap you, will catch you. The same happens with these catch bonds, they bind, and when they are under force, they will not come apart more rapidly, but their survival time under force increases and they remain bound. Simply ingenious. The consequence is that the cluster which consists of catch bonds grows when it is subjected to force. The reason is that the off-rate decreases and a new equilibrium is established by drawing more bonds into the cluster.
![A: Activated state model of a receptor ligand interaction. See text and supp. Info for explanation of parameter. Mean lifetime of an intermolecular bond subjected a constant force showing catch bod behavior shown as a red solid line. B: Conceptual energy landscape of a two-state-two-pathway catch bond. Rapid partitioning between the two ground states occurs without force and the occupancy ratio is determined by the free energy difference between the two states. Pathway switching is assumed to occur if the energy difference between the two bound states shifts in proportion to the applied force as a consequence of a small length ∆x gained in the transition from the slip state to the catch state[6]. Thus, the ratio of the occupancy shifts with an increase in force. If the energy contour of the slip state unbinding pathway points orthogonal to the direction of the applied force, the unbinding kinetics are essentially unaffected. As pointed out by Evans and coworkers, key to the switching mechanism is the small difference in energy levels between the two bound states, which favors the catch pathway over the slip pathway[6]. C: Stability analysis of a pre-stressed catch bond cluster subjected to a sudden perturbation. In contrast to the slip-type, a cluster of catch bonds will remain stable under a constant imposed force. The stable region is highlighted within the white ellipsoid. However, if the force exceeds the stability threshold, the cluster will fail, similar to the slip-bond case. Trajectory visualizes the states of a cluster subjected to two perturbations in the simulation in D. D: Simulation of the evolution of the number of bound ligands (N) and the force felt per molecule (∆F/N) for a catch bond cluster under a sudden perturbation after 45 s and 115 s (green arrowhead). In contrast to the slip bond case, the cluster grows in size initially and draws more ligands into the patch. If the perturbation increases further, the bonds assumes slip bond pathway and the cluster fails catastrophically. The trajectory of the cluster is shown in B.](https://wormwideweb.files.wordpress.com/2014/08/figure-5.jpg)
A: Activated state model of a receptor ligand interaction. Mean lifetime of an intermolecular bond subjected a constant force showing catch bod behavior shown as a red solid line.
B: Conceptual energy landscape of a two-state-two-pathway catch bond. Rapid partitioning between the two ground states occurs without force and the occupancy ratio is determined by the free energy difference between the two states. Pathway switching is assumed to occur if the energy difference between the two bound states shifts in proportion to the applied force as a consequence of a small length ∆x gained in the transition from the slip state to the catch state. Thus, the ratio of the occupancy shifts with an increase in force. If the energy contour of the slip state unbinding pathway points orthogonal to the direction of the applied force, the unbinding kinetics are essentially unaffected. As pointed out by Evans and coworkers, key to the switching mechanism is the small difference in energy levels between the two bound states, which favors the catch pathway over the slip pathway. C: Stability analysis of a pre-stressed catch bond cluster subjected to a sudden perturbation. In contrast to the slip-type, a cluster of catch bonds will remain stable under a constant imposed force. The stable region is highlighted within the white ellipsoid. However, if the force exceeds the stability threshold, the cluster will fail, similar to the slip-bond case. Trajectory visualizes the states of a cluster subjected to two perturbations in the simulation in D. D: Simulation of the evolution of the number of bound ligands (N) and the force felt per molecule (∆F/N) for a catch bond cluster under a sudden perturbation after 45 s and 115 s (green arrowhead). In contrast to the slip bond case, the cluster grows in size initially and draws more ligands into the patch. If the perturbation increases further, the bonds assumes slip bond pathway and the cluster fails catastrophically. The trajectory of the cluster is shown in B.
Relevant Publications:
M Krieg et al. Systemsbiology of mechanosensation. in preparation
M. Krieg, et al. Angew Chem Int Ed Engl, 47(50):9775–7, 2008
A. Kedrov, et al. EMBO Rep, 6(7):668–74, 2005